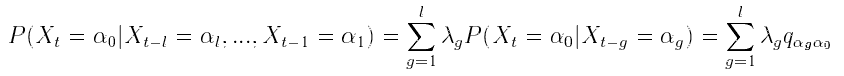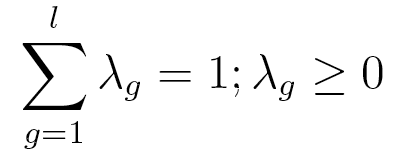YAKUSA overview
YAKUSA (Yet Another K-Uples Structure Analyser) is a program devised to
rapidly scan a structural database with a query protein structure. It
searches for the longest common substructures, called SHSP for
"structural high scoring pairs'', between a query structure and every
structure in the structural database. It makes use of protein backbone
internal coordinates (α angles) in order to describe protein structures
as sequences of symbols. It uses a deterministic finite automaton for
pattern matching. The structural similarity is established in five
steps, the three first ones being analogous to those used in BLAST:
- building-up of a deterministic finite automaton describing all
patterns identical or similar to those in the query structure,
- searching for these patterns in every structure in database,
- selection and extension of these patterns in longer matching
substructures, i.e. the SHSPs,
- selection of compatible SHSPs for each query/database structure
pair,
- ranking of the query/database structure pairs with score based on
SHSP probabilities and spatial compatibility of the SHSPs.Structural
fragment probabilities are estimated by the mixture transition
distribution model, which is an approximation of high order Markov
chain models.
Structures Description
 |
Yakusa is a local structural similarity searching method
that works at the residue Cα level and makes use of the backbone
internal angles. The advantage of internal angles is their simplicity
for describing protein structure at the "local" level.
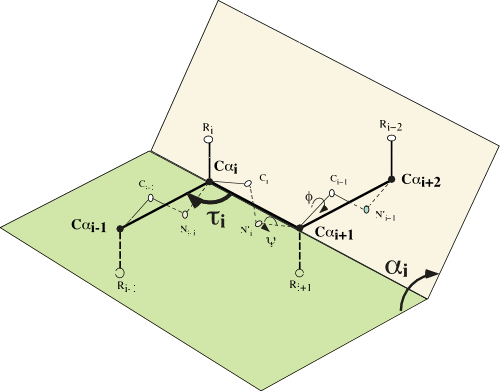
To describe protein structures, we use the α and τ internal angles. The α angle is the
dihedral angle between four consecutive α carbons and τ is the angle
made by three consecutive α carbons (see left). These angles can be
computed from the 3D coordinates of the Cα atoms, and the Cα backbone
can be completely described by α angles, τ angles and distances between
successive Cα. Since τ angles are almost constant and distances between
two Cα are also almost constant (around 3.8 angstrom), protein backbone
structure is accurately described by only α angles. We cluster α angles
into classes over a mesh. We use a 10° mesh, so there are 36
classes of α angles. We represent a class by a numerical symbol (an
integer) and we describe the structure as a run of such symbols. Then
3D backbone structure can be considered as a text and we can apply any
pattern matching algorithms on this "structural text". Therefore, we
consider a protein structure as an internal angle linear sequence; this
description tremendously speeds up similarity searches. Furthermore, as
we are interested only in finding gap-free similar structural "blocks"
in two proteins, we address this problem by examining contiguous
internal angle stretches in them. |
General Algorithm
As protein structures are viewed as texts, the general principle is
first to find all fixed size common patterns (identical or similar)
between the query protein and each database protein. The execution time
for this step is proportional to the length of the protein databas. In
a second stage, most "promising" patterns are selected and extended and
they give rise to the longest similar segments, SHSP, between query and
database structures. The local structural similarities between the
query structure and each database structure are established in five
steps.
- In a first step, the query patterns are put into an automaton to
be used later for the scanning phase. The query is split in overlapping
fixed size patterns filling up the automaton. Not only the automaton
describes exact query patterns but it also contains all patterns
similar to them. The structure of the automaton is the same as the Aho-Corasick's one for multi-pattern searching.
- In a second step, the database structure is scanned with the
automaton. This step exhibits all similar short common patterns, called
"seeds", shared by the query structure and the database structure.
- In a third step, the seeds are selected: for a query/database
pair, there are usually several thousand of seeds, and only the most
"promising" are selected.
- In a fourth step, seeds are extended to the longest possible
SHSPs (Structural High Scoring Pair).
- In the last step, the best "sequentially compatible" SHSPs are
selected and a global score is computed for the query
structure/database structure pair.
All these steps, except the first one, are repeated for each entry of
the structural database. The global score of each query/database
structure pair is used for ranking the results.
Scanning the database
[words in color refer to YAKUSA parameters] The automaton contains
all overlapping fixed length query patterns (seed
length) and all the patterns similar to each of them; they
are called seeds. When seeking protein structural similarities, an α
angle of 20° can be considered as similar to an angle of 30° as
to an angle of 10°, because a difference (degeneracy) between
angles must be taken into account to seek not only for strictly
identical patterns but also for closely related ones. To generate
patterns similar to the ones of the query we introduce a "local degeneracy" at the level of every
pattern symbol. This "local degeneracy" is limited to a maximum local
degeneracy, δmax, and it is expressed
in mesh units. For example, with a 10° mesh, the symbol 2,
represents the interval of α angles between [20°,30°[. When a
δmax=1 is applied, this symbol 2 will be considered similar to the
symbols 1 and 3, which represent respectively the intervals
[10°,20°[ and [30°,40°[. However, for two protein
backbone segments, succession of cumulated small angle differences can
lead to noticeable structure discrepancy. In order to limit the
propagation of this local degeneracy, we define a "global degeneracy" threshold, Δmax. And, for a generated pattern to be
similar to a query pattern, the sum of absolute values of local
degeneracies must be lower than the threshold Δmax, also expressed in
mesh units.
Each database structure, encoded into α angles, is scanned linearly, as
going through the automaton and common seeds are found beetween the
query structure and each database structure. These seeds are gathered,
filtered and extended to SHSPs, which must be longer than a threshold.
The ranking score is based on SHSP probabilities and spatial
compatibility of the SHSPs. The SHSPs "spatial compatibility" is is
based on their RMS. Structural fragment probabilities are estimated by
the mixture transition distribution model, which is
an approximation of high order Markov chain models.
YAKUSA parameters and default values are:
- seed length, default value 5
residues,
- maximum local degeneracy δmax,
default value 3 in mesh unity,
- maximum global degeneracy Δmax,
default value, 7 in mesh unity,
- minimum SHSPs length, default
value 6 residues,
As an option, a filter can be put on canonical α helix. It hides the
middle of α helices but keeps their ends. Helices are hidden during the
search of seeds, but not in the extension step. Therefore, α helices
are finally still found but as they would lead to the generation of
many seeds in first steps, the scan is faster.
Databases available for scanning
- In order to get accurate results and to limit an uninteresting
huge output, we use a non redundant PDB (8742 entries in February
2004), made up of protein structures which:
- are made up of only one PDB chain,
- do not share more than 80% identities in amino-acid
sequences,
- have more than 80 residues.
- Others filtered databases of representative PDB structures can
be used: ASTRAL
databases and Culling databases, at several amino acids identity
rates.
see also a more detailed explanation of
the databases
In protein structures, neighbouring α angles are far from independent,
and correlations between neighbouring angles spread over several
residues. A higher than first order Markov chain modelling of these
dependancies need many more parameters than one could estimate on
available PDB structures. Therefore, we used a Mixture Transition
Distribution Model for high order Markov chains modelling within a
finite state space.
Briefly, the MTD model approximation is a conditional probability
pair approximation. Let 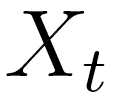 be a random variable in a finite set
be a random variable in a finite set 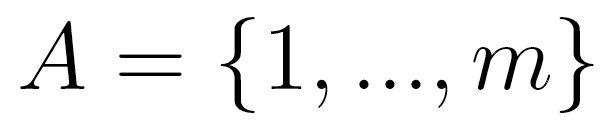 . In an lth order Markov chain,
the probability of
. In an lth order Markov chain,
the probability of 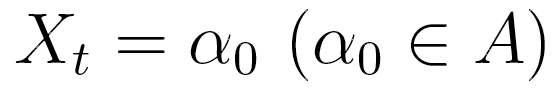 , depends on the combination of values taken by
, depends on the combination of values taken by  . In the MTD
model, the contribution of each lag to the "present" is additive:
. In the MTD
model, the contribution of each lag to the "present" is additive:
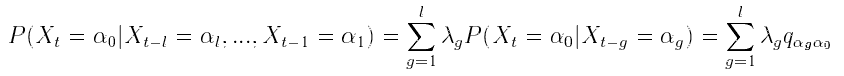
where 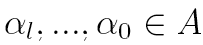 , probabilities
, probabilities 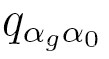 are elements of a
are elements of a 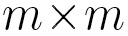 transition matrix
transition matrix 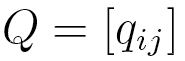 each of whose rows is a probability distribution, and
each of whose rows is a probability distribution, and 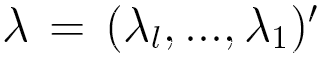 is a vector of lag parameters. To ensure that the results of the model
are probabilities, λ is subject to the two following constraints:
is a vector of lag parameters. To ensure that the results of the model
are probabilities, λ is subject to the two following constraints:
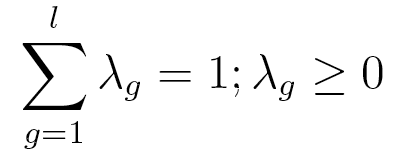
This model has only 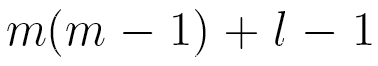 independent parameters, while a Markov chain model needs
independent parameters, while a Markov chain model needs 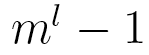 parameters.
parameters.
Here, as a finite set of states, we take the set of α angles
discretized on a 10° mesh (so Q is a 36 x 36
matrix). The MTD model parameters are estimated on the non redundant
PDB structures and we take a l value of 8. To a SHSP is assigned the
probability of the database structural fragment composing this SHSP.
The probability of a structural fragment in the database is computed
from the run of its angles according to the MTD model (for the SHSP 8
first angles, we use a conditonal probability, with l=2). With this MTD
model, the probabilities associated with standard secondary structures,
as α helices, increase and these fragments are therefore more easily
discarded. This allows to bring to the fore interesting fragments
having less standard secondary structures. The ranking score is the sum
of the logarithm of these SHSPs probabilities (x-1, so
they are positive). However, all found SHSPs probabilities are not
always used: by default, only "spatially compatible"
SHSPs are used to compute ranking scores.
Key references for MTD:
- Berchtold, A., A.E. Raftery (2002) The Mixture Transition
Distribution Model for High-Order Markov Chains and Non-Gaussian Time
Series. Statistical
Science, 17 (3), 328-356. (This is a review paper including both
theoretical aspects and applications of the MTD model.)
- Berchtold, A. (2001) Estimation in the Mixture Transition
Distribution Model. Journal of Time Series Analysis, 22(4),
379-397. (Description of a new
estimation algorithm for the computation of the finite space version of
the MTD
model.)
- Le, N.D., R.D. Martin, A.E. Raftery (1996) Modeling Flat
Stretches, Bursts, and Outliers in Time Series
Using Mixture Transition Distribution Models. Journal of the
American Statistical Association, 91,
1504-1515. (Generalization of the MTD model to general state
spaces.)
- Raftery, A.E. (1985) A model for high-order Markov chains.
Journal of the Royal Statistical Society B, 47 (3),
528-539. (Paper introducing first the MTD model.)
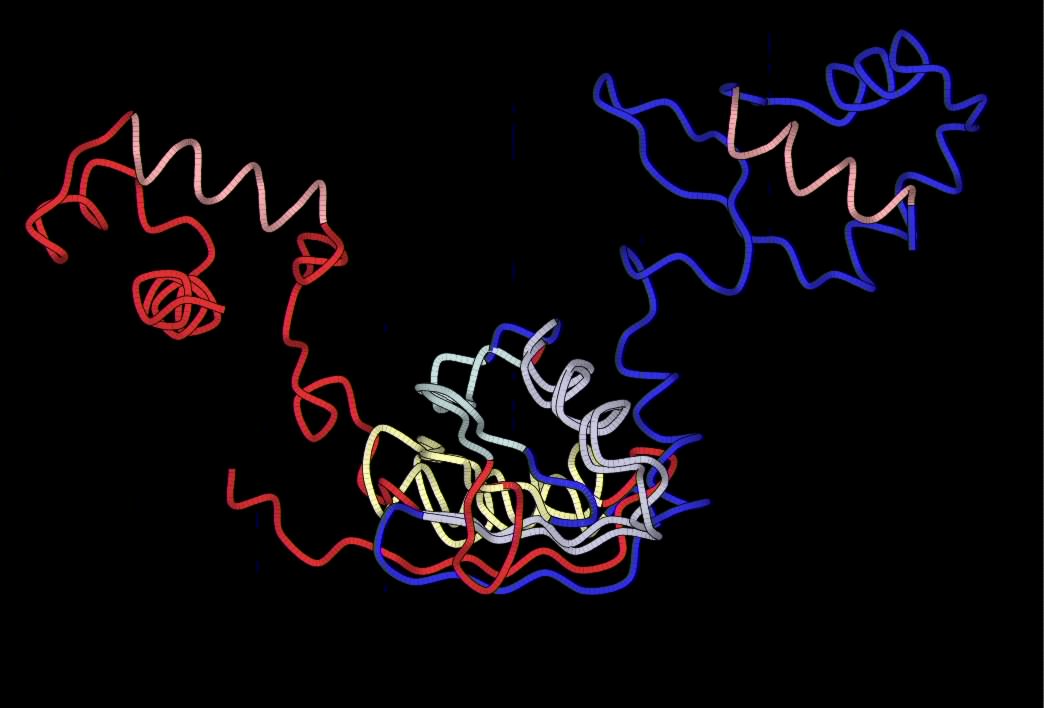
|
YAKUSA have found four SHSPs but only 3 of them are
"spatially compatible", the purple
, green and yellow ones. If
the two
structures are aligned on the cyan SHSP, other SHSPs RMS ()are very
high, while if they are aligned on the three others SHSPs (on this
figure, they are aligned on the green one), RMSs are low execpt for the
cyan SHSP. We compute RMS of all SHSPs for each spatial alignment:
|
SHSP Id for RMS |
SHSP Id
for alignment |
1 |
2 |
3 |
4 |
| 1 |
0.4 |
39.6 |
14.0 |
24.2 |
| 2 |
39.9 |
1.2 |
1.7 |
7.4 |
| 3 |
55.2 |
6.2 |
0.9 |
8.9 |
| 4 |
26.9 |
9.0 |
5.9 |
1.7 |
SHSPs are considered in the same group when all their RMSs are below a
threshold (15 Angstrom by default). |
| In red, 1i1g (chain A), crystal structure of the lrp-like
transcriptional regulator from the archaeon pyrococcus furiosus.
In blue, 1b4a (chain F) structure of the arginine repressor from
bacillus stearothermophilus. |
|
Last modified: Tue Dec 7 18:18:43 CET 2004