Hidden Markov Model Structural alphabet (SA-HMM) for the exploration of protein structures
Introduction
Understanding and predicting protein structures depends on the
complexity and the accuracy of the models used to represent them. An
emerging concept of the stuctural biology is the identification of a
Structural Alphabet i.e. of a limited number of recurrent structural
elements of proteins, structural "letters", whose associations
governed by logic rules form the words of protein structures. The
definition of such an alphabet poses numerous technical problems, but
provides a new tool for better understanding protein architecture. In
addition, the applications possible from such alphabet are numerous and
range from simplifying the protein backbone conformation with a correct
accuracy to more ambitious prediction approaches.
Hidden Markov Model
(HMM) was used to discretize protein backbone
conformation as series of overlapping fragments (states) of 4-residue
length
Camproux, 1999a.
Using
HMM allows
moving the description of 3D structures from the sole geometric aspect
towards a more explanatory description embedding local dependence
information. This results in both a library of
representative structural fragments and their first order dependency,
called Structural Alphabet (
SA). The question
of how many different representative fragments can optimally decompose
the whole set of short local conformations occurring in protein
structures can be adress using a statistical criterion. An optimal
systematic decomposition of the conformational variability of the
protein peptidic chain is obtained in 27 states together with strong
connection logic,stable over different protein sets.
SA-
HMM fits well the
previous knowledge related to protein architecture organisationand
seems able to grab some subtle details of protein organisation, such as
helix sub-level organisation schemes. Encoding protein 3D
coordinates into the fragments library or "structural alphabet space"
(
SA) allows to discretize the 3D architecture ofproteins in terms of a
1-dimensional
SA, noted 1D'
SA. Reconstruction 3D of proteins
from 1D'
SA space is validated on a set of proteinsand compared to
recent approaches. Use of
HMM allows to drastically reduce the
complexity of the reconstruction. Although we use short fragments, the
learning process on entire protein conformations captures the logic of
the assembly on a larger scale. Using such a model, the structure of
proteins can be reconstructed with an average accuracy close to
1.1 Amgstroms of RMSd and for a complexity of only 3. Finally, we also observe
that sequence specificity increases with the number of states of the
structural alphabet. Such models can constitute a very relevant
approach to the analysis of protein architecture in particular for
proteinstructure prediction.
Materials and Methods
Material
The extraction of SA is performed
from a collection of 1429 non-redundant proteins structures with
no disorder presenting less than 30% sequence identitywith a
resolution better than 2.5 Amgstrom. In order to keep a balance between the
largest number of proteins selected for learning and the
representativity of the dataset, we have used the non-redundant
set presenting less than 30% sequence identity. Only proteins at least
30 amino acids long, having no chain breaks, obtained by X-ray.
This resulted in a collection of 1429 proteins with no disorder or
missing coordinates.
Describing three dimensional
conformations
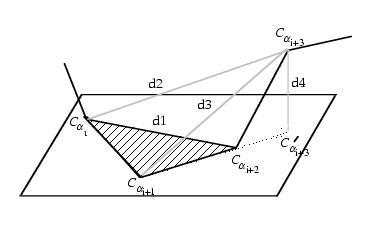
The structures are described as consecutive overlapping fragments
of 4-residues so that they can be fitted together to form the backbone
geometry
Camproux, 1999b. Each fragment is described by
a 4-descriptors vector: the three distances between the non consecutive
alpha_carbons : d
1=d{C
alpha1-C
alpha3},
d
2=d{C
alpha1-C
alpha4},
d
3=d{C
alpha3-C
alpha4}
where 1,..,4 denotes the 4 residues of a fragment, and the oriented
projection P_4 of the last alpha-carbon C_alpha
4(h)
to the plane formed by the three first ones. Two independent learning
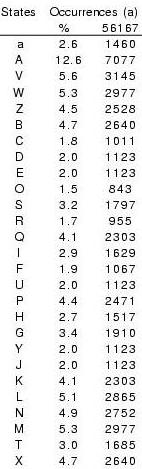
subsets of 250 proteins representing respectively a total of 56167
four-residues fragments (LS1) and 57544 four-residues fragments (LS2)
were randomly selected.
Results
Identification of the optimal
structural alphabet (SA)
Suppose we knew that
polypeptidic chains are made up of representative fragments of R
different types. We would then assume that there are (R) states of the
model. Each state corresponding to a representative 4-residue fragment
of the polypeptidic chains is associated with a multinormal function.
Two models are considered: (i) a process without memory (order 0),
assuming independence of the R states and identified by training simple
finite Mixture Models (MM); (ii) a process
with memory, i.e., a markovian model of order 1, where dependence
between contiguous fragmentsidentified by training a HMM,
see (Rabiner, 1989). Since HMM or MM give a
quantification of the likelihood of the data in the terms of a model,
it is possible to compare models using statistical criteria such as
Bayesian Information Criterion (BIC), (Schwartz, 1978).
Structural alphabets of different size (R), noted SA-R were learnt using
HMM by progressively increasing R and compared
using BIC
Combining HMM or MM with statistic criterion allows us to find
the optimal library fragments size from parsimony point of view.
The difference between the two types of models either HMM
(Markovian dependence between the states) or MM (independence), compare
on the basis of their goodness of fitis striking. For MM, no optimum is
reached until alphabet sizes of 70 whereas for HMM, an optimum is
reached for a number of states of 27 (SA-27) meaning a better fit of
the data using HMM.
Hence, learning prototype conformations considering not only the
geometry of the fragments but also the way the fragments are
concatenated (Markovian dependence) results in a simpler description,
in the sense that the optimal description of protein conformations can
be done using a much smaller number of prototype conformations. Similar
results (Figure 1) were obtained using two independent learning sets of
250 proteins (referred to as LS1 and LS2). The optimum is reached
for 27 states in both cases, and we find that the states identified
from LS1 and LS2 are very similar in terms of averages, variabilities,
frequencies and transitions.
Optimal Structural Alphabet
Geometrical description of the SA
Conformational variability of 4-residue fragments of proteins is
optimally described by a SA of 27 representative fragments, labelled
as [A,B,...,Z, a] Camproux, in revision. They are sorted by increasing stretches of their corresponding fragments and generated using XmMol (Tuffery, 1995).
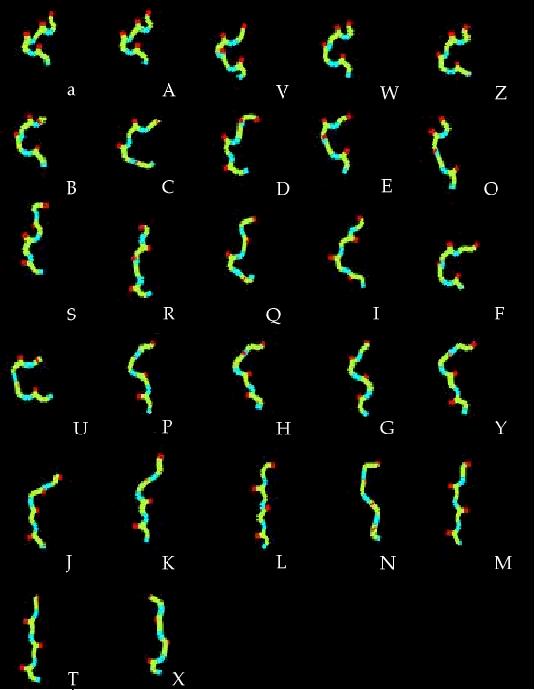
Interestingly, identified fragments are similar
on two independent sets of proteins, confirming identified fragments
library represents well the conformational space of local fragments.
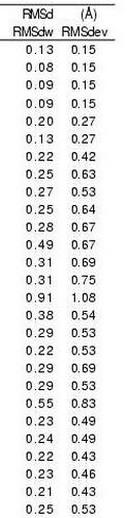
Good RMSd is found on each of the 27 representative fragments (in
average 0.23 A). Moreover, the geometries of the fragments associated
with the 27 states are distinguishable. The 27 states are, on average,
significantly different from each other for at least 3 descriptors.
Also, the average alpha-carbon RMSd between fragments associated with
different states (RMSd_dev) are all larger than the RMSdw values.
The correspondence between the
states and the usual secondary structures motifs (as identified using
the STRIDE software, Frishman, 1995), is presented.
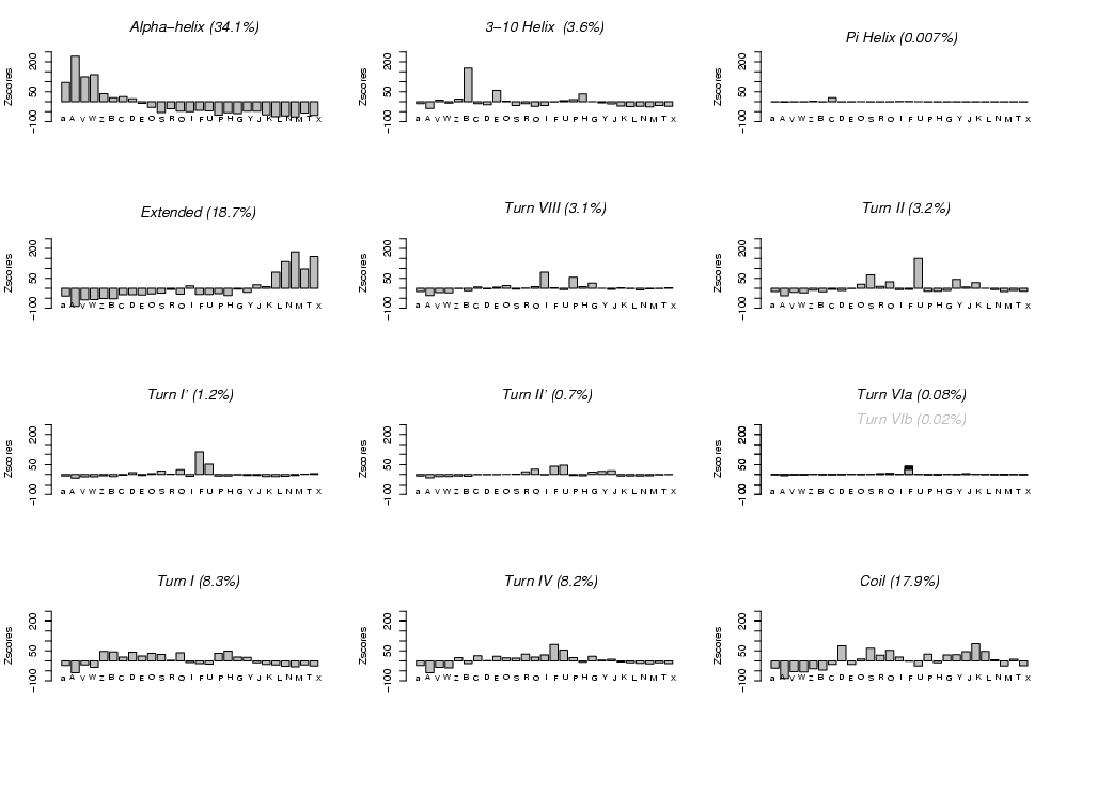 Note that we have a much larger number of states than the
secondary structure categories, and that we describe the conformations of fragments of 4-residue length (i.e. local shapes).
Also, usual secondary structures are defined according to geometry criteria, and not the logic underlying the
succession of the conformations. Finally, it is possible that for example single helix-like conformations
can be observed outside helices. Hence we do not expect a strict correspondence here.
However, we observe some clear relationships.
Canonical alpha-helices are mostly associated with states [A, a, V, W] (the shortest states),
but some positive over-representation of states [Z, B, C, D] is also observed.
In contrast, 3-10 helices
are mostly described by state [B], and to a lesser extent by states [E, H].
Pi-helices - only 0.7% of the dataset - seem to correspond to state [C].
Extended structures are dispatched into five states [L, N, M, T, X].
beta-turns, are associated with one or few particular states.
Turns VIII (3.1%) correspond to states [I, P, G]
and turn II (3.2%) mostly to states [U, S].
Turn I' and turn II' correspond both to fuzziest state [F] and to
its closest state [U]. Turns VIa and VIb, occurring few, correspond to state [F].
The remaining Turn I, Turn IV, as well as the Coils, correspond to more
complex profiles of states, clearly different however.
Turn I (8.3%) is associated with
several states [Z, B, C, D, E, O, S, Q, P, H].
Turn IV (8.2%), a geometrically not well determined turn,
correspond to states [R, Q, I, F, U, G], among which states [F, R] are the
geometrically most variable states.
The remaining coils (17.9%) are mostly described by states
[G, Y, J, K, L] corresponding to rather extended conformations
and by states [D, S, Q].
Note that we have a much larger number of states than the
secondary structure categories, and that we describe the conformations of fragments of 4-residue length (i.e. local shapes).
Also, usual secondary structures are defined according to geometry criteria, and not the logic underlying the
succession of the conformations. Finally, it is possible that for example single helix-like conformations
can be observed outside helices. Hence we do not expect a strict correspondence here.
However, we observe some clear relationships.
Canonical alpha-helices are mostly associated with states [A, a, V, W] (the shortest states),
but some positive over-representation of states [Z, B, C, D] is also observed.
In contrast, 3-10 helices
are mostly described by state [B], and to a lesser extent by states [E, H].
Pi-helices - only 0.7% of the dataset - seem to correspond to state [C].
Extended structures are dispatched into five states [L, N, M, T, X].
beta-turns, are associated with one or few particular states.
Turns VIII (3.1%) correspond to states [I, P, G]
and turn II (3.2%) mostly to states [U, S].
Turn I' and turn II' correspond both to fuzziest state [F] and to
its closest state [U]. Turns VIa and VIb, occurring few, correspond to state [F].
The remaining Turn I, Turn IV, as well as the Coils, correspond to more
complex profiles of states, clearly different however.
Turn I (8.3%) is associated with
several states [Z, B, C, D, E, O, S, Q, P, H].
Turn IV (8.2%), a geometrically not well determined turn,
correspond to states [R, Q, I, F, U, G], among which states [F, R] are the
geometrically most variable states.
The remaining coils (17.9%) are mostly described by states
[G, Y, J, K, L] corresponding to rather extended conformations
and by states [D, S, Q].
Logical rules within Structural Alphabet
Sparse transition matrix betwen states enclosed in the Markovian model
revealed strong dependence between fragments. This table shows Markov transition, i.e. probability to transit from state i (column) to state j (row) with (*) corresponding to frequency less than 1% and more than 0.1%. 
Taking advantage of this local dependence reduces both the total number
of representative fragments and number of possible
representative fragments at each position (average of 8 states).
Structures encoding in SA space
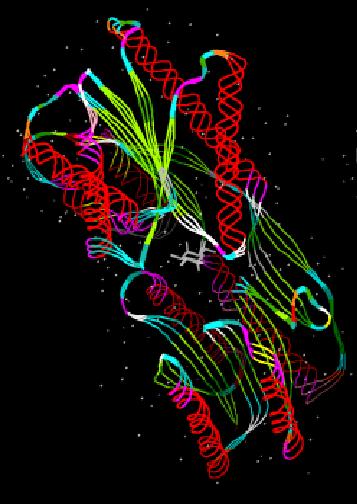
Encoded 3D conformation proteins
in the 1D'
SA space corresponds to a compression of the 3D-protein
space in the discrete
SA space (1D').
aking into account dependence between fragments allows to perform this
encoding globally and non position by position and to reduces the
complexity of the reconstruction. Indeed, Viterbi algorithm
(Baum, 1970; Rabiner, 1989) based on dynamic programming algorithm, finds the
single best fragments series amongst all possible paths.
Reconstruction of 3D conformation of
proteins from 1D'
SA space corresponds to the decompression step.
Quality of the reconstruction step is evaluated on a sample of 200
proteins and shows very performent results considering very low
complexity, compared to to recent approaches Micheletti (2000), Kolodny (2002).
Using such a model, the structure of proteins can be reconstructed with
an average accuracy close to 1.1 Amgstroms of RMSd and for a complexity of only 3.
Subsequently,
SA provides some kind of compression from the 3D protein coordinate space
into a 1D structural alphabet space. From such 1D encoding and the associated logical rules,
it seems possible to tackle the exploration of three-dimensional
protein conformations using 1D techniques.
An facility coming with the use of
HMM is that it is possible to quantify,
during the
SA encoding of proteins of known structures,
the probability of substituting one local conformation by another.
This allows to quantify the similarity of protein fragments encoded as different series of states.
This widens the perspective of being able to work with a 1D representation of 3D structures
much beyond the simple search of exact words, through the use of the classical 1D amino acid
alignment methods.
Conformational learning correlates with sequence specificity
We have assessed the degree of specificity of the sequences associated with each state of SA-27.All the states have some significant amino acid sequence specificity compared to the profiles of the collection of 1429 protein fragments.Using a Kullback-Leibler asymmetric divergence measure, the weakest dependence, observed for [E], is still very significant (p<0.001). This implies that the distributions of the 4-uplets of amino acids associated with each state become more and more specific as the number of states increases. This confirms that, despite we have learnt SA using only geometric information, we have not over-split sequence information.
Conclusion
This approach can be used for
analysing strings of conformational states that define protein
structure in the same way that is done for strings of amino acid
residues that define protein sequence. For instance to generate
accurate loop conformations in homology modelling (
Camproux, 2001), for homology search
and for prediction ab initio from the discretize conformational space.
 The structures are described as consecutive overlapping fragments
of 4-residues so that they can be fitted together to form the backbone
geometry Camproux, 1999b. Each fragment is described by
a 4-descriptors vector: the three distances between the non consecutive
alpha_carbons : d1=d{Calpha1-Calpha3},
d2=d{Calpha1-Calpha4},
d3=d{Calpha3-Calpha4}
where 1,..,4 denotes the 4 residues of a fragment, and the oriented
projection P_4 of the last alpha-carbon C_alpha4(h)
to the plane formed by the three first ones. Two independent learning
subsets of 250 proteins representing respectively a total of 56167
four-residues fragments (LS1) and 57544 four-residues fragments (LS2)
were randomly selected.
The structures are described as consecutive overlapping fragments
of 4-residues so that they can be fitted together to form the backbone
geometry Camproux, 1999b. Each fragment is described by
a 4-descriptors vector: the three distances between the non consecutive
alpha_carbons : d1=d{Calpha1-Calpha3},
d2=d{Calpha1-Calpha4},
d3=d{Calpha3-Calpha4}
where 1,..,4 denotes the 4 residues of a fragment, and the oriented
projection P_4 of the last alpha-carbon C_alpha4(h)
to the plane formed by the three first ones. Two independent learning
subsets of 250 proteins representing respectively a total of 56167
four-residues fragments (LS1) and 57544 four-residues fragments (LS2)
were randomly selected. 


 Note that we have a much larger number of states than the
secondary structure categories, and that we describe the conformations of fragments of 4-residue length (i.e. local shapes).
Also, usual secondary structures are defined according to geometry criteria, and not the logic underlying the
succession of the conformations. Finally, it is possible that for example single helix-like conformations
can be observed outside helices. Hence we do not expect a strict correspondence here.
However, we observe some clear relationships.
Canonical alpha-helices are mostly associated with states [A, a, V, W] (the shortest states),
but some positive over-representation of states [Z, B, C, D] is also observed.
In contrast, 3-10 helices
are mostly described by state [B], and to a lesser extent by states [E, H].
Pi-helices - only 0.7% of the dataset - seem to correspond to state [C].
Extended structures are dispatched into five states [L, N, M, T, X].
beta-turns, are associated with one or few particular states.
Turns VIII (3.1%) correspond to states [I, P, G]
and turn II (3.2%) mostly to states [U, S].
Turn I' and turn II' correspond both to fuzziest state [F] and to
its closest state [U]. Turns VIa and VIb, occurring few, correspond to state [F].
The remaining Turn I, Turn IV, as well as the Coils, correspond to more
complex profiles of states, clearly different however.
Turn I (8.3%) is associated with
several states [Z, B, C, D, E, O, S, Q, P, H].
Turn IV (8.2%), a geometrically not well determined turn,
correspond to states [R, Q, I, F, U, G], among which states [F, R] are the
geometrically most variable states.
The remaining coils (17.9%) are mostly described by states
[G, Y, J, K, L] corresponding to rather extended conformations
and by states [D, S, Q].
Note that we have a much larger number of states than the
secondary structure categories, and that we describe the conformations of fragments of 4-residue length (i.e. local shapes).
Also, usual secondary structures are defined according to geometry criteria, and not the logic underlying the
succession of the conformations. Finally, it is possible that for example single helix-like conformations
can be observed outside helices. Hence we do not expect a strict correspondence here.
However, we observe some clear relationships.
Canonical alpha-helices are mostly associated with states [A, a, V, W] (the shortest states),
but some positive over-representation of states [Z, B, C, D] is also observed.
In contrast, 3-10 helices
are mostly described by state [B], and to a lesser extent by states [E, H].
Pi-helices - only 0.7% of the dataset - seem to correspond to state [C].
Extended structures are dispatched into five states [L, N, M, T, X].
beta-turns, are associated with one or few particular states.
Turns VIII (3.1%) correspond to states [I, P, G]
and turn II (3.2%) mostly to states [U, S].
Turn I' and turn II' correspond both to fuzziest state [F] and to
its closest state [U]. Turns VIa and VIb, occurring few, correspond to state [F].
The remaining Turn I, Turn IV, as well as the Coils, correspond to more
complex profiles of states, clearly different however.
Turn I (8.3%) is associated with
several states [Z, B, C, D, E, O, S, Q, P, H].
Turn IV (8.2%), a geometrically not well determined turn,
correspond to states [R, Q, I, F, U, G], among which states [F, R] are the
geometrically most variable states.
The remaining coils (17.9%) are mostly described by states
[G, Y, J, K, L] corresponding to rather extended conformations
and by states [D, S, Q].

 Encoded 3D conformation proteins
in the 1D' SA space corresponds to a compression of the 3D-protein
space in the discrete SA space (1D').
aking into account dependence between fragments allows to perform this
encoding globally and non position by position and to reduces the
complexity of the reconstruction. Indeed, Viterbi algorithm
(Baum, 1970; Rabiner, 1989) based on dynamic programming algorithm, finds the
single best fragments series amongst all possible paths.
Reconstruction of 3D conformation of
proteins from 1D' SA space corresponds to the decompression step.
Quality of the reconstruction step is evaluated on a sample of 200
proteins and shows very performent results considering very low
complexity, compared to to recent approaches Micheletti (2000), Kolodny (2002).
Using such a model, the structure of proteins can be reconstructed with
an average accuracy close to 1.1 Amgstroms of RMSd and for a complexity of only 3.
Encoded 3D conformation proteins
in the 1D' SA space corresponds to a compression of the 3D-protein
space in the discrete SA space (1D').
aking into account dependence between fragments allows to perform this
encoding globally and non position by position and to reduces the
complexity of the reconstruction. Indeed, Viterbi algorithm
(Baum, 1970; Rabiner, 1989) based on dynamic programming algorithm, finds the
single best fragments series amongst all possible paths.
Reconstruction of 3D conformation of
proteins from 1D' SA space corresponds to the decompression step.
Quality of the reconstruction step is evaluated on a sample of 200
proteins and shows very performent results considering very low
complexity, compared to to recent approaches Micheletti (2000), Kolodny (2002).
Using such a model, the structure of proteins can be reconstructed with
an average accuracy close to 1.1 Amgstroms of RMSd and for a complexity of only 3.