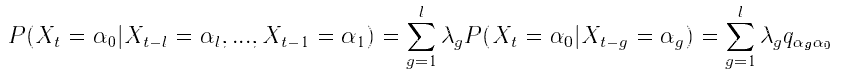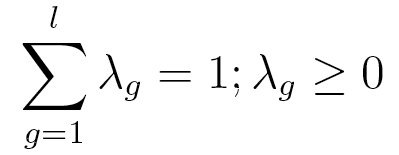YAKUSA overview

1. building-up of a deterministic finite automaton describing all patterns identical or similar to those in the query structure,
2. searching for these patterns in every structure in database,
3. selection and extension of these patterns in longer matching substructures, i.e. the SHSPs,
4. selection of compatible SHSPs for each query/database structure pair,
5. ranking of the query/database structure pairs with score based on SHSP probabilities and spatial compatibility of the SHSPs.Structural fragment probabilities are estimated by the mixture transition distribution model, which is an approximation of high order Markov chain models.

Structures Description

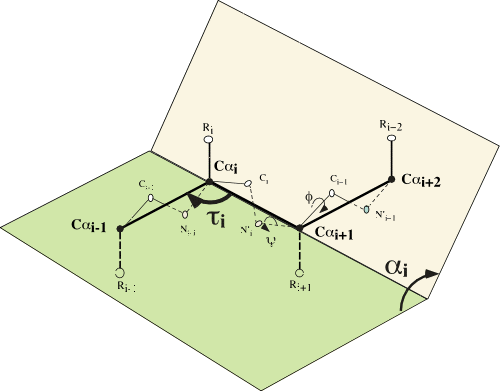
Yakusa is a local structural similarity searching method that works at the residue Cα level and makes use of the backbone internal angles. The advantage of internal angles is their simplicity for describing protein structure at the "local" level. To describe protein structures, we use the α and τ internal angles. The α angle is the dihedral angle between four consecutive α carbons and τ is the angle made by three consecutive α carbons (see left). These angles can be computed from the 3D coordinates of the Cα atoms, and the Cα backbone can be completely described by α angles, τ angles and distances between successive Cα. Since τ angles are almost constant and distances between two Cα are also almost constant (around 3.8 angstrom), protein backbone structure is accurately described by only α angles. We cluster α angles into classes over a mesh. We use a 10° mesh, so there are 36 classes of α angles. We represent a class by a numerical symbol (an integer) and we describe the structure as a run of such symbols. Then 3D backbone structure can be considered as a text and we can apply any pattern matching algorithms on this "structural text". Therefore, we consider a protein structure as an internal angle linear sequence; this description tremendously speeds up similarity searches. Furthermore, as we are interested only in finding gap-free similar structural "blocks" in two proteins, we address this problem by examining contiguous internal angle stretches in them.

General Algorithm

• In a first step, the query patterns are put into an automaton to be used later for the scanning phase. The query is split in overlapping fixed size patterns filling up the automaton. Not only the automaton describes exact query patterns but it also contains all patterns similar to them. The structure of the automaton is the same as the Aho-Corasick's one for multi-pattern searching.
• In a second step, the database structure is scanned with the automaton. This step exhibits all similar short common patterns, called "seeds", shared by the query structure and the database structure.
• In a third step, the seeds are selected: for a query/database pair, there are usually several thousand of seeds, and only the most "promising" are selected.
• In a fourth step, seeds are extended to the longest possible SHSPs (Structural High Scoring Pair).
• In the last step, the best "sequentially compatible" SHSPs are selected and a global score is computed for the query structure/database structure pair.

Scanning the database

YAKUSA Parameters

• seed length, default value 5 residues,
• maximum local degeneracy δmax, default value 3 in mesh unity,
• maximum global degeneracy Δmax, default value, 7 in mesh unity,
• minimum SHSPs length, default value 6 residues,

Databases available for scanning

1. In order to get accurate results and to limit an uninteresting huge output, we use a non redundant PDB (8742 entries in February 2004), made up of protein structures which:
   • are made up of only one PDB chain,
   • do not share more than 80% identities in amino-acid sequences,
   • have more than 80 residues.
2. Others filtered databases of representative PDB structures can be used: ASTRAL databases and Culling databases, at several amino acids identity rates.

MTD

In protein structures, neighbouring α angles are far from independent, and correlations between neighbouring angles spread over several residues. A higher than first order Markov chain modelling of these dependancies need many more parameters than one could estimate on available PDB structures. Therefore, we used a Mixture Transition Distribution Model for high order Markov chains modelling within a finite state space.

Briefly, the MTD model approximation is a conditional probability pair approximation. Let 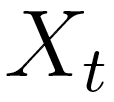be a random variable in a finite set 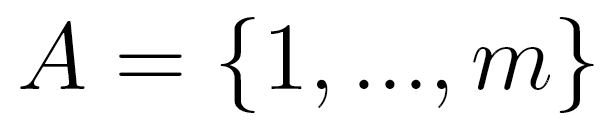. In an lth order Markov chain, the probability of 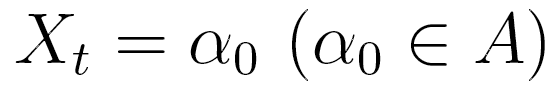, depends on the combination of values taken by . In the MTD model, the contribution of each lag to the "present" is additive:
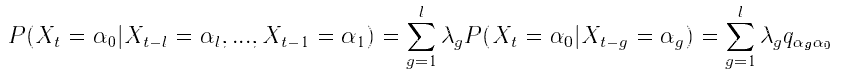
where 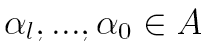, probabilities 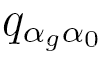are elements of a 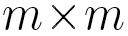transition matrix 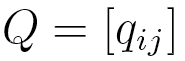each of whose rows is a probability distribution, and 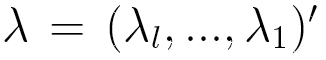is a vector of lag parameters. To ensure that the results of the model are probabilities, λ is subject to the two following constraints:

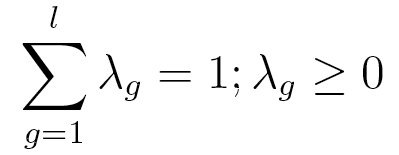
This model has only 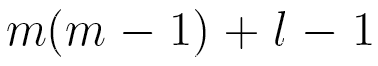independent parameters, while a Markov chain model needs 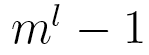parameters.

Here, as a finite set of states, we take the set of α angles discretized on a 10° mesh (so Q is a 36 x 36 matrix). The MTD model parameters are estimated on the non redundant PDB structures and we take a l value of 8. To a SHSP is assigned the probability of the database structural fragment composing this SHSP. The probability of a structural fragment in the database is computed from the run of its angles according to the MTD model (for the SHSP 8 first angles, we use a conditonal probability, with l=2). With this MTD model, the probabilities associated with standard secondary structures, as α helices, increase and these fragments are therefore more easily discarded. This allows to bring to the fore interesting fragments having less standard secondary structures. The ranking score is the sum of the logarithm of these SHSPs probabilities (x-1, so they are positive). However, all found SHSPs probabilities are not always used: by default, only "spatially compatible" SHSPs are used to compute ranking scores.

Key references for MTD:

• Berchtold, A., A.E. Raftery (2002) The Mixture Transition Distribution Model for High-Order Markov Chains and Non-Gaussian Time Series. Statistical Science, 17 (3), 328-356. (This is a review paper including both theoretical aspects and applications of the MTD model.)
• Berchtold, A. (2001) Estimation in the Mixture Transition Distribution Model. Journal of Time Series Analysis, 22(4), 379-397. (Description of a new estimation algorithm for the computation of the finite space version of the MTD model.)
• Le, N.D., R.D. Martin, A.E. Raftery (1996) Modeling Flat Stretches, Bursts, and Outliers in Time Series Using Mixture Transition Distribution Models. Journal of the American Statistical Association, 91, 1504-1515. (Generalization of the MTD model to general state spaces.)
• Raftery, A.E. (1985) A model for high-order Markov chains. Journal of the Royal Statistical Society B, 47 (3), 528-539. (Paper introducing first the MTD model.)

Spatial compatibility

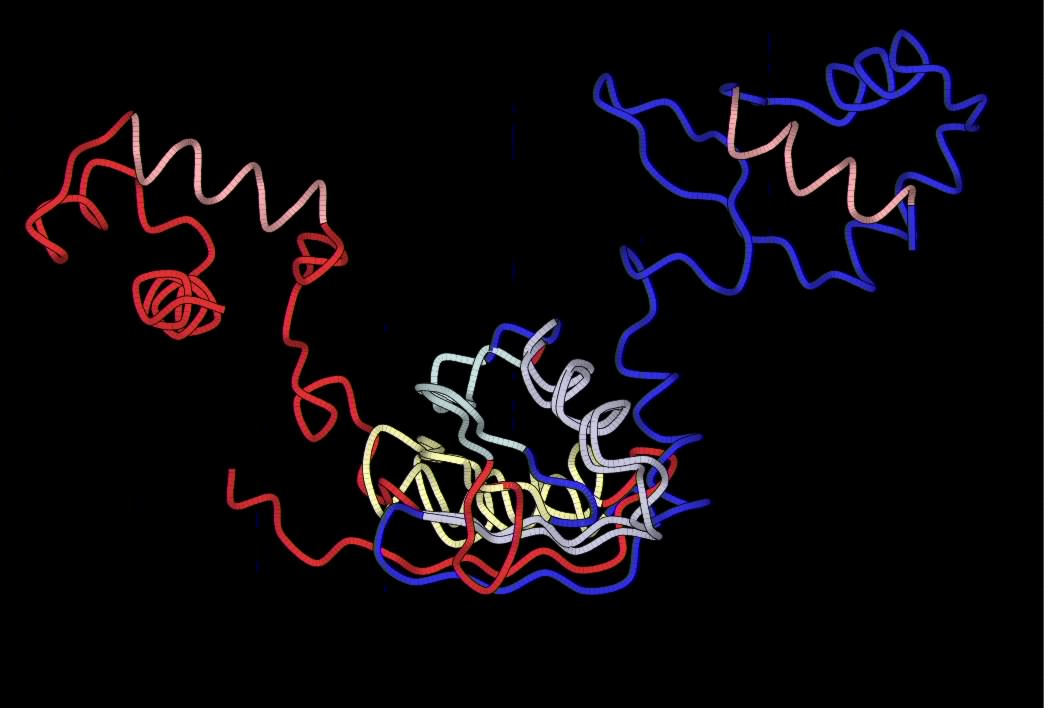
YAKUSA have found four SHSPs but only 3 of them are "spatially compatible", the purple ,  green and yellow ones. If the two structures are aligned on the cyan SHSP, other SHSPs RMS ()are very high, while if they are aligned on the three others SHSPs (on this figure, they are aligned on the green one), RMSs are low execpt for the cyan SHSP. We compute RMS of all SHSPs for each spatial alignment: SHSP Id for RMS SHSP Id for alignment 1 2 3 4 1 0.4 39.6 14.0 24.2 2 39.9 1.2 1.7 7.4 3 55.2 6.2 0.9 8.9 4 26.9 9.0 5.9 1.7 SHSPs are considered in the same group when all their RMSs are below a threshold (15 Angstrom by default).

In red, 1i1g (chain A), crystal structure of the lrp-like transcriptional regulator from the archaeon pyrococcus furiosus. In blue, 1b4a (chain F) structure of the arginine repressor from bacillus stearothermophilus.